To find the low resistance by Carey Fosters Bridge Experiment Setup

Objective / Aim of the Experiment

To find the low resistance by Carey Fosters Bridge Experiment Setup

Apparatus Required

Low Resistance
DC Power Supply (2V)
Carey Fosters Bridge Setup
Galvanometer
One way key

Formula Used

X = (d₂Y₁ - d₁Y₂) / (d₂-d₁)

Circuit Diagram of Carey Foster Bridge Experiment

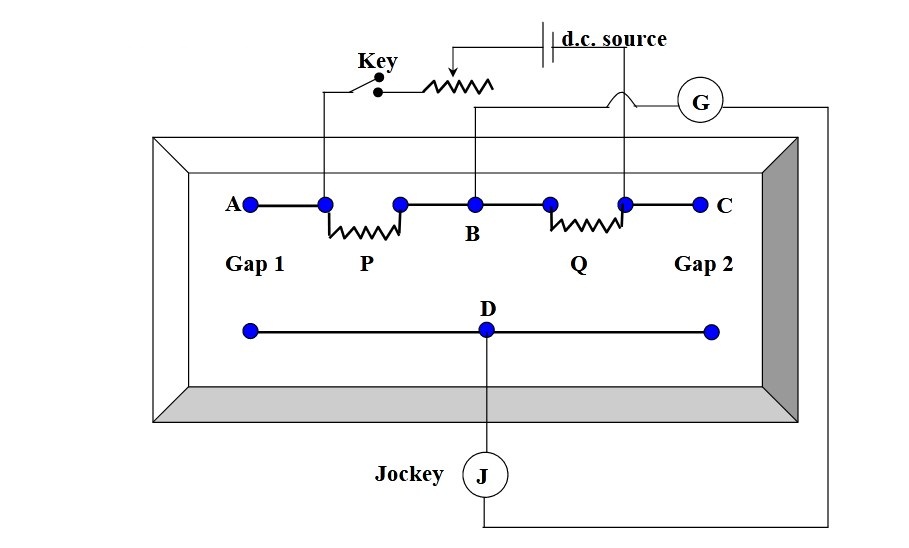
Theory

Carey Fosters bridge is a modified Wheatstone bridge. Here a potentiometer wire MN is inserted between the R and S arms of the Wheatstone bridge as shown in Figure above. The ratio arms P & Q are made equal. Gap 1 carries a small resistance (known) and the Gap 2 (fourth arm) carries the unknown resistance. If ρ be the resistance per unit length of wire, r₁ & r₂ be the end resistances at M & N, MD = l₁ is balancing length a shown in figure.

then P / Q = (X + l₁ρ + r₁) / [Y + (100-l₁)ρ + r₂] ............. (1)

When, X & Y are interchanged, the balance point shifts to a length ₂, then,

then P / Q = (Y + l₂ρ + r₁) / [X + (100-l₂)ρ + r₂] ............. (2)

Comparing (1) & (2) and adding 1 to both sides, we get,
Y - X = (l₁ - l₂)ρ

Where X is unknown resistance, (l₁ - l₂) is shift in balance point when the positions of X & Y are interchanged. Let d₁ & d₂ are the shifts corresponding to resistances Y₁ & Y₂, then,

X - Y₁ = d₁ρ and X - Y₂ = d₂ρ, so, (X - Y₁) / (X - Y₂) = d₁ / d₂

X = (d₂Y₁ - d₁Y₂) / (d₂-d₁)

Procedure

1. Make connection as shown in the figure.

2. Fix P = Q = 1 Ω throughout the experiment.

3. Keep X = Y = 0 by short circuiting by copper plates to get balance point.

4. Repeat step (iii) by interchanging the position of copper plates and determine x 0 .

5. Replace trip of gap 1 by unknown resistance X and gap 2 by known resistance Y. Find balance point for 0.1 Ω, and, then interchange X & Y, and, again find balance point.

6. Repeat this step for Y = 0.2, 0.3, 0.4, 0.5 Ω.

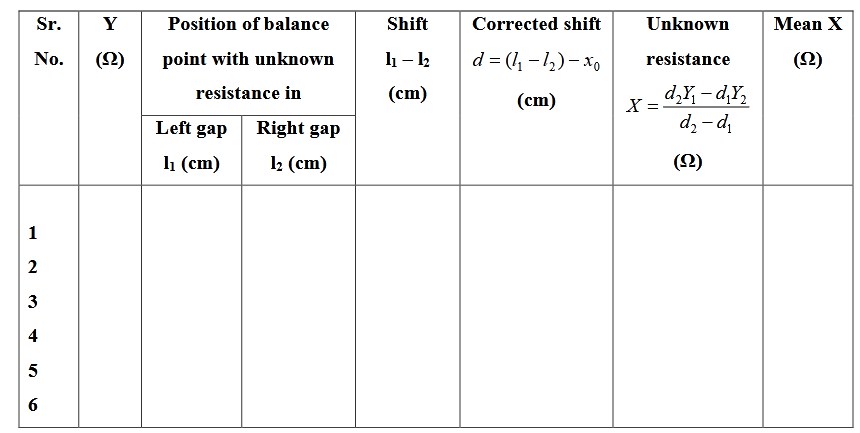
Observations

(a) Determination of electrical zero:

(a) Determination of unknown resistance:

Result

The value of unknown resistance is .............. Ω.

Precautions

• All terminals should be tight.
• The connecting wires and the copper strip should be thoroughly cleaned with sand paper.
• The connection should be tight and the plugs of the resistance box should be given twist so that they are tight.
• The battery key should be taken out when the readings is not being taken in order to avoid heating and the wire.

Carey Fosters Bridge Viva Questions and Answers

Question-1: What do you mean by the resistance of a conductor?
Answer-1: The ratio of the potential difference between the two ends of a conductor to the current flowing in it, is called the resistance of a conductor.

Question-2: On what factor does it depends?
Answer-2: Resistancve of a conductor is directly proportional yo its length(l), inversely proportional to the area of cross section (A). It also depends upon the nature of material and temperature of the conductor.

Question-3: What is its unit?
Answer-3: Unit if resistance is ohm.

Question-4: What is effect of temperature on resistance?
Answer-4: It increases with the increase in temperature.

Question-5: What is the effect of increasing the effective length of a Carey Fosters bridge wire?
Answer-5: It will increase the accuracy of the result because then percentage error in reading the position of the balance point is very much decreased.

Question-6: What is the minimum difference in resistance that you can measure with this bridge wire?
Answer-6: It is equal to the resistance of the one millimeter length of the bridge wire.

Tags:

Image Credits: Freepik